GEORGE FRIEDRICH BERNHARD RIEMANN (1826-1866). Gran matemático alemán. Realizó numerosas contribuciones a varias ramas de las matemáticas, siendo las más conocidas en Geometría no Euclídea, ecuaciones diferenciales y teoría de números. Sus hallazgos fueron fundamentales para el desarrollo posterior de la Teoría Especial de la Relatividad de Einstein.
La suma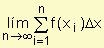 
que aparece en la definición de integral definida se llama suma de Riemann en honor a este matemático . Su definición incluía además subintervalos de distinta longitud.
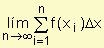que aparece en la definición de integral definida se llama suma de Riemann en honor a este matemático . Su definición incluía además subintervalos de distinta longitud.
Cuatro de los métodos de suma de Riemann para aproximar el área bajo las curvas. Los métodos derecha e izquierda hacen la aproximación usando, respectivamente, los puntos finales derechos e izquierdos de cada subintervalo.
Los métodos máximo y mínimo hacen la aproximación usando, respectivamente, los valores más grandes y más pequeños del punto final de cada subintervalo. Los valores de las sumas convergen a medida que los subintervalos parten desde arriba a la izquierda hasta abajo a la derecha.
No hay comentarios:
Publicar un comentario