La suma de Riemann puede interpretarse como una suma de áreas de los rectángulos de aproximación.
Esto se debe a una partición de un intervalo [a, b] es un conjunto finito de puntos [a, b] que incluye a los extremos. Arbitraria de dicho intervalo a = x0 £ x1 £ x2 £ x3 £ ......... £ xn-1 £ xn = b donde D xi indica la amplitud o longitud del i-ésimo subintervalo. Si ti es cualquier punto del i-ésimo subintervalo la s
uma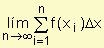 
xi-1 £ ti £ xi se llama suma de Riemann de f asociada a la partición.
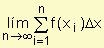xi-1 £ ti £ xi se llama suma de Riemann de f asociada a la partición.
No hay comentarios:
Publicar un comentario