R/ La derivada consiste en la RAZÓN DE CAMBIO de una función real o compleja de una variable
2.¿En que consiste la integral?
R/ la integral es el proceso de cálculo de áreas encerradas entre una curva y un eje cartesiano
3.¿En que consiste el área?

El tamaño de una superficie.La cantidad de espacio dentro de los límites de un objeto plano (bi-dimensional).
4.¿Que relación hay entre la derivada y la integral?

R/ Consiste en la PRIMITIVA DE UNA FUNCIÓN O ANTIDERIVADA, osea cuando conocemos una función F, pretendemos encontrar otra función F que cumpla la condición F'= F
5.¿En que consiste la suma de Riemann?
R/ Consiste en un método de integración numérica que sirve para calcular el valor integral definida es decir el área bajo la curva.
Básicamente se refiere a trazar un número finito de rectángulos dentro de un área irregular, calcular el área de cada uno de los rectángulos y sumarlos.
6.¿Que perrequisitos se deben tener en cuenta par proceder a las Sumas de Riemann?
7.¿Una vez terminado de ver sumas de rieman "calculo integral" a que pasariamos?

8. Que entiende por el teorema fundamental del calculo?
R/ Cualquiera de las diferentes técnicas elementales usada para calcular una antiderivada o una integral indefinida de una función.
Así que una función f(x) por el teorema fundamental del cálculo equivale a hallar una función f(x) tal que f(x) es su derivada.














 limite [0,3]
limite [0,3]




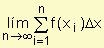








 .
.
 .
.